|

Theory of the correspondence of music and image
Drawing the diagram for transfer
of melodies of 4, 8, and 12 bars
The center of diagram is correlated with the conditional
lowest note (it is assumed that human ear can not distinguish notes
with value below 20-25 Hertz). Therefore, the conditional inaudible
octave is represented by the empty square in the center. The size
of first working octave is calculated through the 1:2
proportion on the "note pitch" coordinate.

Proportion 1:2 corresponds to the correlation of the
note frequencies in the octave. Compare, for example, "La"
note of the different octaves: 220 Hertz, 440 Hz, 880 Hz. The same
is true for other frequencies of notes – when rising by the octave
the note frequency has the doubled value (true for the even-tempered
system).
Further, we divide the first working octave into twelve
paths (corresponding to 12 semitones of octave).
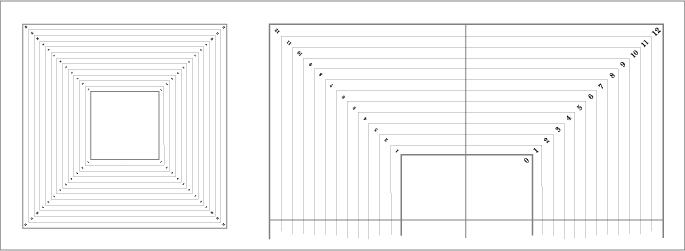
Motion can be started from any diagonal. The motion
can be counterclockwise or clockwise. (However, in all examples
the beginning point will be the upper right diagonal, and the motion
will be counterclockwise).
Since the melodies usually cover two octaves, we have
to add on the outside the space for the higher octave by the same
principle (preserving the proportions of external square to the
first internal one).
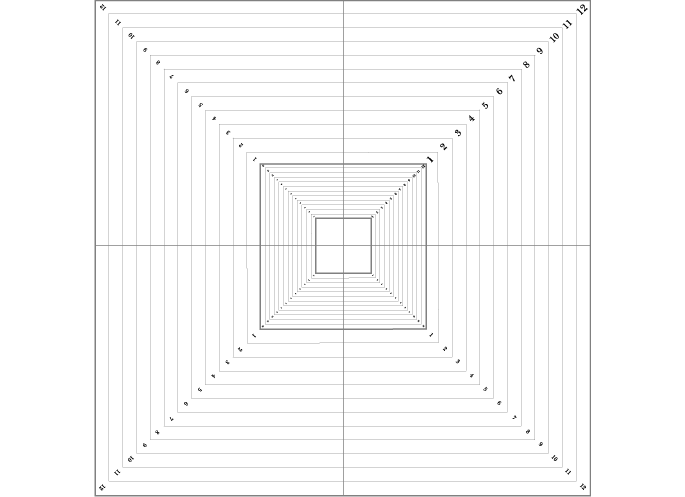
Now the tonality of musical composition is to be determined
– in the diagram the note representing the tonality corresponds
to paths 0 and 12. With "La" tonality, for example, path
2 will be intended for "Si" note, while with "Do"
tonality path 2 will be intended for "Re" note..
When the notes are transferred to the appropriate
paths with observance of "time" coordinate, the points
are connected with the lines smoothed by the Bezie Curves principle.
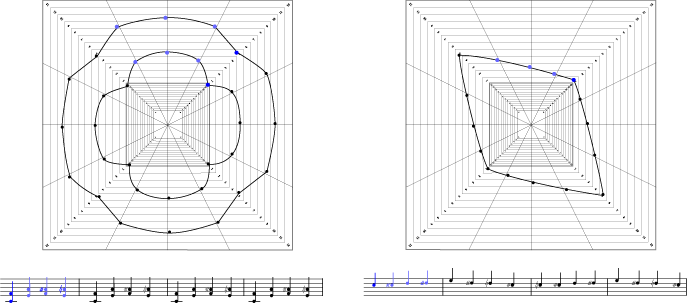
go to the results
of transfers of sonic to the plane...
return to the previous
page
Auxiliary explanations
Curves of Bezie
Rules of the connections of the transferred points
Arrangement of color on the plane
|













